变化的牛顿常量：一部标量张量理论的个人史
——关于爱因斯坦广义相对论中引力常数并非常量的修正
来源于https://www.einstein-online.info/en/spotlight/scalar-tensor/
原文标题: Varying Newton’s constant: A personal history of scalar-tensor theories
惯性和引力
宇宙的巧合？
如果G不是常量会怎么样？
1/G是标量场
通往标量张量理论
标量场的兴衰
标题中“变化的…常量”这样矛盾的说法，首次被我使用于1961年我在普林斯顿的博士论文中。其中，我发展了一种清晰的对爱因斯坦理论的修正——提出一个变化的标量场来决定牛顿万有引力“常数”G。这些想法是最先由狄克（R. H. Dicke）分享给我，而他此前为马赫（Mach）,狄拉克（Dirac）等人的想法所鼓舞。在1961年，我们首次发布关于这个主题的我们的理论。尽管P. Jordan和他的同事们已经更早地独立发展了他们的一套理论。最终，这些理论本该理所当然的被称为“Jordan- Brans-Dicke,” (JBD，约尔当—布兰斯—狄克宇宙论)。但不幸的是，很多论文忽视了Jordan开创性的工作，并且引用时仅仅称其为“Brans-Dicke”（布兰斯—狄克宇宙论）。更客观的术语应该是”标量张量理论“（scalar-tensor theories or ST theories）。
在爱因斯坦诞生前几个世纪，常量G首次出现于经典引力中。1687年，牛顿发表了他的万有引力理论。万有引力将天文现象（如行星绕太阳轨道运行）统一进我们在地球上日常生活对重力，引力的认识。源于开普勒对行星运动的分析，牛顿用他的力学定律表明所有物质都存在一种相互吸引的力。这种力正比于二者质量的乘积，且反比于他们距离的平方。对我们来说，这里的关键词是“成比例“。牛顿用他手中的数据做出了成比例的最好描述。直到1798年英国科学家卡文迪许完成了一个相当困难的实验——在实验室中确切地测量了两个已知质量已知间距的物体之间微小的力，我们才得到最早的比例系数，也就是G的估计值。
今天，我们知道不论在实验室还是太阳系中G都约为6.7×10-11m3/(kg·s-2)。但是，G真的是一个常量吗，还是G是一个关于宇宙中物质分布的函数？这就是最终引出一系列被称为标量张量理论的问题，我们即将在这篇文章中讨论。
惯性和引力
在创立广义相对论的过程中，爱因斯坦深深地着迷于物理学家所说的惯性力与牛顿引力之间的共性。如果你不容易头晕，你可以自己体验一下一个惯性力的典型例子。站起身，两只手臂自然垂在身体两侧，然后以身体为轴，将脚尖旋转。你将体会到一种被称为“离心力” 的惯性力把你的手臂向外拉。
惯性力和引力有一个特别有趣的相似点。惯性力（比如离心力）正比于被拉住的物体的质量。对引力来说也是如此，而引力将物体向地球拉拽。这个力（也叫重力）也正比于他作用的物体的质量。
为什么会有这样的相似之处？是否正如奥地利物理学家、哲学家马赫推测的那样，这些相似之处隐藏了某种深层的联系？惯性力是否是一种由遥远恒星施加的特殊引力作用吗？那些处于宇宙其他地方绕着我们旋转的遥远星系和作用在我们手臂上的力之间是否存在因果关系？
事实上，早在1912年爱因斯坦就发表了一篇论文，提到了马赫的工作对他的引力思想的影响。大约三年后，爱因斯坦发表了他的引力理论，广义相对论。他认为广义相对论符合马赫关于惯性和引力的观点。在20世纪20年代，爱因斯坦宣称广义相对论甚至可以明确地显示惯性力是如何依赖于宇宙的总体质量分布。爱因斯坦在证明这个主张所用的宇宙模型在大小上是有限的，这个空间类似于半径为R的三维球体表面，其总质量为M。有趣的是，根据爱因斯坦的论点，惯性力和总体质量分布之间的关系，只有在M,R和牛顿万有引力常数G满足一个特殊关系的时候才成立，即
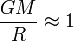或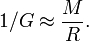
在这里我们选择了以秒为单位来度量时间和空间（长度的一秒，也被称为一光秒，是光在一秒内走过的距离）。
最终，爱因斯坦以错误的方式仅仅将惯性力归因于遥远星系的作用。这并不意味着惯性力和引力之间的关系不重要。只是核心问题不再是惯性力是否由遥远星系产生，而是另一项爱因斯坦在发展其理论时广泛使用的性质：如物理学家所说，惯性力可以被“变换消去“。具体而言，惯性力可以通过转换参考系消去（在前面的例子中，是从旋转者的参照系转换到一个没有旋转的参照系）。引力同样如此，如果你进行自由落体运动，重力可以在局部和近似下被消去。
宇宙的巧合？
宇宙学的发展很快淘汰了爱因斯坦的静态有限宇宙观。从20世纪30年代起，追随着美国天文学家哈勃（Edwin Hubble）和胡马森（Milton Humason）的观测结果，我们逐渐清晰地认识到，我们生活在一个不断膨胀的、无限的宇宙中。距现在一段有限的时间之前（约138.2亿年前），我们的宇宙从一个被称为大爆炸的极热而稠密的初始状态中产生。然而，即使在这样的宇宙观下，联系G和宇宙的大小和质量的等式似乎依然成立，尽管R和M的意义有所不同：在一个诞生于有限时间之前的宇宙中，天文学家无法观测到最大距离R之外的物体。简单来说，这是因为来自宇宙更远的地方的光没有足够的时间抵达地球。将你所能看到最大距离范围内的所有物体质量表示为M。随着观测宇宙学的发展，至少从20世纪30到50年代的数据来看，这个方程对我们的宇宙的确仍是近似有效的。
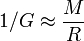
现在我们回过头来思考，这个关系的实质究竟只是一个无比惊人的数据上的宇宙学巧合，还是表明之前爱因斯坦提出的预言关系是正确的——牛顿引力常数依赖于宇宙的总体质量分布！
首先，为什么说这是一个“令人惊讶”的巧合呢？在一个膨胀的宇宙中，宇宙可观测部分的半径R随时间增加——随着时间推移，来自更遥远地方的光可以到达我们这里。宇宙可观测部分物质的质量也在增加，但这从某种程度上意味这意味着M/R这个比值也随时间变化。如果G是个常量，并且M/R随时间变化，那么方程
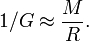
只能近似地在一段很短的时间内成立，而这段时间相对于漫长的宇宙历史而言非常短。这正是巧合所在，这段时间正好重合于人类可以利用强力的望远镜观测太空，并且发现膨胀宇宙的数学模型的时候。
在后来被称为“大数假说”的背景下，这只是狄拉克在20世纪30年代末研究的一系列明显的数学巧合之一。狄拉克怀疑，事实上这一切绝不仅是巧合。在他发展的宇宙学中，我们的方程表示了G,M和R之间的系统性关系。
从现代观点来看，狄拉克的宇宙学只不过是一个历史的注脚。但在标量张量理论背景下，这引出了一系列丰富的新观点：如果G,M和R是相关联的，且M/R随时间变化，那么G也不可能是常量。
如果G不是常量会怎么样？
事实上，上述方程给出的M,G和R的关系，不禁让人联想到另一种物理定律。我们先暂时抛开引力一会，来考虑一个电荷。只要给出电荷的电势，V，我们就能表示出其对周围电荷的作用（V的单位为伏特）。在空间中的每个点都对应特定的电势。用物理的话来说，这是一个电势场。此外，这个值仅仅是一个数值（相对的，只用一个数值无法表示力，你需要同时指出其大小和方向）。物理学家称这种场为“标量场”。
大多数读者都熟悉电势的一种特殊应用。电池的“力量”用其“电势”来衡量，这也正是电池两极的差异所在。有趣的是，一个带点粒子附近的势是由这个公式决定的。
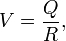
Q是粒子电荷量，R是粒子与指定点的距离。这个方程看起来非常像我们已经发现的，已经出现在前文的那个方程，只不过是换成了对1/G。这两个方程中，右端都有一个“电荷”（电荷又或是质量，作为“引力电荷”）除以一个长度。这暗示着1/G本身是一个标量场，其当前值取决于给定时间内可观测宇宙的质量和其他性质。
请注意，我们并不是说1/G应该被看做电势，并且明确地取决于电荷。我们只是指出两个方程在形式上的相似之处。
1/G是一个标量场
1/G是一个标量场意味着什么？结果看上去很矛盾，这意味着G是一个变化的引力常数——它也根本不需要是常数而且很可能随时间变化。原则上说，它会随时间和空间的变化而变化。
引力常数取决于宇宙质量分布的观点并不符合爱因斯坦广义相对论的公式。因此理论需要被推广；新理论除了原有的“度规场”外，还包含了一个标量场。度规场是时空几何编码的数学对象。在数学上，度规场是一种叫“张量”的东西（对数学家来说，这个名称表现了不同观察者使用不同坐标系对几何的看法）。因此，既包含度规场又包含标量场的理论统称为标量张量理论。
在广义相对论框架中，新的场为标量场是一个很重要的信息。在爱因斯坦理论中，引力场可以被“变换消去”。至少在局部，引力可以被消去。例如，设想一个在地球引力场中自由下落的实验室。在实验室中释放的物体将静止“悬浮”于空中，与地面保持恒定的距离。这是因为物体和地面都在以相同的加速度朝地球加速。所以，实验室中的观察者将断言，物体是“不受重力”的，这样引力就被“消去”了。现实中，在环绕卫星上的“失重”宇航员不断地体验着这样的观测。更多详情可以参考这篇文章《电梯，火箭和重力：等效原理》（The elevator, the rocket and gravity: The equivalence principle）。标量场无法用同样的方式变换消去。因此，它具有一种持久性，这种持久性与它依赖于一个整体的量（如可观测宇宙的质量）相协调。
通往标量张量理论
在广义相对论中假设1/G是一个标量场是一回事，但真正建立一个描述这种标量场动力学理论又是另外一回事。对于此，最初的奠基性的工作是由两个科学家在探索完全不同的另一个问题时做出的。在爱因斯坦广义相对论发展的早期（最初几年），德国物理学家，数学家卡鲁扎（Theodor Kaluza）和瑞典物理学家克莱因（Oskar Klein）提出了一个爱因斯坦引力和电磁学的统一描述，这个模型应当将两种相互作用描述为同一个广义几何结构的结果。结果表明，这种模型不仅产生了引力和电磁场，而且还自动包含一个额外的场，这个场的作用是1/G并且满足一个近似于我们在之前讨论的那个方程。
卡鲁扎-克莱因理论并没有很好地如预期那般统一引力和电磁学，也没有被广泛接受。然而，其中的一些观点在20世纪40到50年代在德国被约尔当（Pascual Jordan）和他的同事重新拾起。利用卡鲁扎-克莱因理论中一个特殊形式的额外标量场，他们建立了一个完整的标量-张量理论，从而推广了爱因斯坦的理论。
同时，由于二战期间美国和德国之间明显缺乏学术交流，爱因斯坦那时和他的助手彼得·伯格曼在新泽西州普林斯顿高等研究院也提出了一个关于G的标量场。然而，爱因斯坦没有深究这个想法，并且美国当时现有的标量张量理论的工作很大程度上被忽略，直至20世纪50年代末。
之后，变化的G的观点又出现于剑桥，丹尼斯西阿玛（Dennis Sciama后来成为富有影响力的相对论专家，当时只是一个研究生），在此提出一个模型，解释了惯性力只出现在相对遥远星系加速的参考系。变化的引力常数并不是西阿玛有意为之。事实上，他提出的模型只是沿着马赫原理（将惯性力表示为引力）的一个推论。然而从结果来看，西阿玛模型的一个重要结果就是我们之前遇到的等式，即
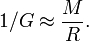
西阿玛的模型被物理学家称为玩具模型——一个简化的模型，虽然它成功的抓住了（并且加深了我们的理解）一个物理情况的特殊方面，但没有成功地描述那个情况的所有方面。西阿玛的模型只在一些特殊情况下推导出牛顿定律，并且不能以一种简单的方式描述光的传播。然而，这个模型为马赫原理提供了新思路，并且因此成为后来发展的重要基石。
我们回到20世纪50年代末的普林斯顿大学，迪克（Robert Dicke）当时是一个主要的，活跃的，关于在理论上和实验上重新检验标准广义相对论的拥护者。特别是受到西阿玛模型和其他关于惯性力的观点以及狄拉克的大数猜想，迪克向我提议（布兰斯，当时是一个理论物理的研究生），探索出一个模型，加入一个“变化引力常数”来推广标准爱因斯坦理论。迪克还提出了额外的必需的条件。第一，这个模型将保证能量动量守恒。就像在经典物理和广义相对论中，不可能有能量或动量凭空产生或凭空消失。第二，模型应当得出一个关联G和宇宙整体性质的方程，类似于我们在前面已经引用的方程。
在那时，我并不知道约尔当沿着这些路线的工作。我独立发展了自己的形式，并且在1960年彻底完成我的论文。由此产生的理论恰当地被称为“约尔当-布兰斯-迪克”宇宙论，或者简称为JBD（Jordan- Brans-Dicke）理论。更广泛接受的叫法是标量张量（ST）理论
爱因斯坦的引力场来源于质量和能量（参考文章《从质量迈向更多Mass and More》）。在JBD理论中，标量场（传统上用希腊字母φ表示），也来源于质量和能量（尽管存在不同之处——与电磁场相关的质能是引力的来源，但不直接对标量场有贡献）。由此，我们可以推断出，在可观测宇宙部分，φ≈M。并且φ/R在描述以质量为源的引力的方程中，其值近似为1/G，引出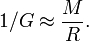，这个读者现在已经完全不陌生的方程。这些理论提出了爱因斯坦广义相对论的一个主要模型。
我们已经提到了一个基本的不同：在ST理论中，不是所有的引力效应都可以像在自由下落的电梯中那样被消除。更准确的说，ST理论对物体和光在引力场中运动和传播的预测可能与广义相对论不同，不同之处在于与无量纲参数ω成反比的项。在为ST理论写出方程的时候，我面临着一个熟悉的问题，即φ与引力和质量的“耦合”。这就需要物理学家所说的“耦合常数”。最终，（结果让迪克大为吃惊）我们的理论用另一个ω替代了未定常数G。并且似乎没有别的办法了。实验人员可以用他们的结果来对ω设限，到目前为止的结果表明，ω必须取使得ST理论在太阳系背景下几乎与爱因斯坦理论难以区分的值。然而，正如下面所讨论的，这些结果并不影响ST理论在宇宙学或量子背景中的潜在重要性。
标量场的兴衰
由于两种理论相似却对物理现象的预言存在轻微的不同，在过去的四十年里，ST理论最终成为第一个重要的对爱因斯坦理论的挑战。迪克接下来做了很丰富的工作以传播这类爱因斯坦理论的替代品，激发了其他学者寻求和进行观测来区分开两种模型。巧合的是，NASA在那时正在寻找能利用太空项目的重要实验。显然，挑战爱因斯坦理论成为了一个诱人的目标。
接下来的实验和观测，既有检验爱因斯坦理论基本假设的（比如等效原理），也有其替代品们对太阳系中行星轨道以及光的传播的预言。事实证明，标准爱因斯坦理论在这些测试中比其他任何替代品都表现的更好。结果，在20世界70年代，大家对这类替代理论兴趣大减。然而，从80年代开始，新发现和新理论重新引起了对标量张量引力的兴趣。
在天文背景下，更多证据表明在宇宙早期存在所谓的暴涨阶段。在这个阶段，宇宙经历过极快的加速膨胀。这有助于解释某些我们宇宙的可观测性质，比如大尺度下各向同性。在现在的模型中，暴涨膨胀是由一个叫暴涨的标量场驱动的，这可以由JBD理论描述。物理学中一个基本的开放性问题是量子引力——一个正在进行的能调和广义相对论和量子理论概念的研究。量子引力理论的候选者之一是弦理论，他假定对于物理学所有已知的基本粒子，如果你能看的足够仔细的话，只是同一种基本一维物体的不同方面，叫做弦。弦理论包含了引力，但它必然伴随着所谓的膨胀，这可能是标量张量理论的标量场在完全不同和出乎意料的背景下的再现。
从这些发展来看，很有可能标量张量引力不必要用来解释天文学家在太阳系里的观测结果，而是在我们对宇宙开端、物质的更基本性质的理解中发挥重要作用。
作者简介：
卡尔.H.布兰斯（Carl H. Brans）
新奥尔良洛约拉大学理论物理学的j·c·卡特名誉教授。他是广义相对论的扩展——约尔当-布兰斯-迪克理论的共同发明人之一。最近，他又在被称为微分拓扑的数学分支领域中，参与了对最近奇异发现的物理意义的研究。
翻译：吴迅，华中科技大学物理学院2020级本科生
编校: 邹远川
文章编号：华中大天文210704
